Celestial Coordinates and Time: RA/Dec, Alt‑Az, LST

Table of Contents

• Introduction
• Why Multiple Sky Coordinate Systems Exist
• Altitude–Azimuth (Alt‑Az) Coordinates
• Equatorial Coordinates: Right Ascension and Declination
• Astronomical Timekeeping: Solar vs Sidereal, UTC, TAI, TT
• Precession, Nutation, Proper Motion, and Epochs
• Ecliptic and Galactic Coordinates
• The Equation of Time and the Analemma
• Practical Conversions: From RA/Dec to Alt‑Az
• Refraction, Parallax, and Apparent Place
• Tools, Standards, and Reliable Data Sources
• FAQs: Concepts and Definitions
• FAQs: Observer and Planning Questions
• Conclusion

Introduction

The sky is a sphere to the eye, but a maze to the unprepared. Astronomers navigate it using coordinate systems anchored to physical reference planes and well-defined time standards. If you have ever wondered why telescopes and star charts use right ascension and declination while your planetarium app shows altitude and azimuth, or why catalogs list positions “J2000” instead of “today,” this guide is for you.

We will build a complete picture of celestial coordinates—from the horizon-based Alt‑Az system to the rotation-oriented Equatorial system (RA/Dec), and onward to the solar system’s Ecliptic frame and the Milky Way–aligned Galactic frame. Along the way, we will pin these geometries to the clock: sidereal time, solar time, UTC, TAI, and TT. We will also discuss the astronomical motions—precession and nutation, proper motion, and aberration—that make the sky a moving target, and the atmospheric and topocentric corrections (refraction and parallax) needed to match calculation with reality.

Our goal is practical mastery: we will provide step-by-step logic for converting RA/Dec to altitude and azimuth, explain why solar noon drifts across the year, and point you to robust tools and standards in software and almanacs. Whether you are a student, an observer in the field, or a developer building astronomy features, understanding coordinates and timekeeping is key to getting the sky right.

Why Multiple Sky Coordinate Systems Exist

Coordinates encode a choice of reference plane and axis. No single choice is optimal for all questions. Different tasks invite different frames:

• Local observing: The horizon-based Altitude–Azimuth system answers: “Where do I look from here and now?”
• Star catalogs and tracking: The Earth’s rotation axis defines the Equatorial system (Right Ascension and Declination). This frame is stable enough to index the sky and drive equatorial mounts.
• Solar system dynamics: The plane of Earth’s orbit defines the Ecliptic system, useful for planetary positions and zodiacal geometry.
• Galactic structure: The Milky Way’s plane defines the Galactic system, best for mapping interstellar gas, star-forming regions, and large-scale Galactic surveys.

On top of these geometric choices, astronomical timekeeping threads the needle between the mean Sun, the distant stars, and atomic clocks. Sidereal time aligns your meridian with the stars; civil time (UTC) keeps society synchronized; dynamical time (TT) underpins precise solar system ephemerides. We will return to these in Astronomical Timekeeping.

Rule of thumb: choose the frame aligned with the phenomenon you are studying, then transform to the frame aligned with your instrument or catalog.

Altitude–Azimuth (Alt‑Az) Coordinates

The Alt‑Az system is anchored to your horizon. It is intuitive and local:

• Altitude (Alt): Angle above the geometric horizon, from 0° (horizon) to +90° (zenith). Below the horizon is negative altitude.
• Azimuth (Az): Compass bearing along the horizon, typically measured from true north (0°) through east (90°), south (180°), west (270°), back to north (360°).

Strengths of Alt‑Az:

• Directly answers “where to point” at a given time and location.
• Used by dobsonian mounts and many computerized mounts (which internally convert from RA/Dec).
• Works naturally with compass bearings and horizon landmarks.

Limitations:

• Time-dependent. Alt‑Az changes from minute to minute as Earth turns.
• Location-dependent. The same star will have different Alt‑Az at different latitudes and longitudes.
• Atmospheric refraction. Near the horizon, refraction can lift objects by ~35 arcminutes (more in unusual conditions). See Refraction.

Calculate Alt‑Az by first determining the star’s hour angle (HA) from local sidereal time and its right ascension, then projecting onto the local horizon plane. We outline the workflow in Practical Conversions.

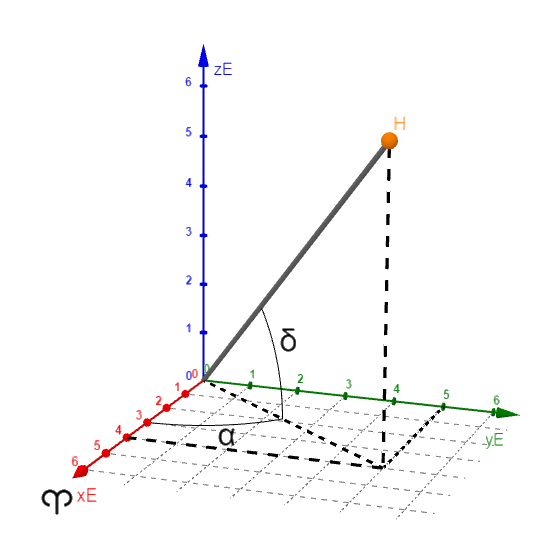
Equatorial Coordinates: Right Ascension and Declination

The Equatorial system is centered on Earth and aligned with its rotation axis. It is the language of star catalogs and equatorial mounts. Its coordinates:

• Declination (Dec): Angular distance north (+) or south (−) of the celestial equator, from −90° (south celestial pole) to +90° (north celestial pole).
• Right Ascension (RA): Eastward angle along the celestial equator from the vernal equinox direction. RA is traditionally measured in hours, minutes, and seconds (24h around the full circle).

RA/Dec are quasi-inertial coordinates ideal for publishing positions. However, they are defined for a particular epoch—a reference date of the equator and equinox. Modern catalogs commonly use J2000.0 (Julian epoch 2000 January 1, 12:00 TT). Because of precession and nutation, the equatorial grid slowly shifts over time; consequently, “of date” coordinates differ from J2000 by tens of arcminutes across centuries.

Equatorial mounts exploit RA/Dec by tracking with a single motor at the sidereal rate: approximately one rotation per sidereal day (≈ 23h 56m 4s). This cancels Earth’s rotation for celestial objects, holding them steady in the field of view, a concept crucial for long-exposure observing and imaging even if you prefer Alt‑Az mounts for their simplicity.

Key concepts linked to Equatorial coordinates:

• Hour Angle (HA): The angular distance westward from your meridian to the object. HA = LST − RA. It is central to the conversion to Alt‑Az.
• Meridian transit: When HA = 0, the object culminates; it typically reaches maximum altitude then, a prime time to observe.
• Circumpolarity: At latitude φ, stars with Dec ≥ 90° − φ never set; those with Dec ≤ −(90° − φ) never rise.

Astronomical Timekeeping: Solar vs Sidereal, UTC, TAI, TT

Time in astronomy connects Earth’s rotation to the stars and the ephemerides of planets. There are three pillars to understand:

Sidereal vs Solar Day

• Sidereal day: The time for Earth to rotate 360° relative to the distant stars: about 23h 56m 4.0905s. Because Earth orbits the Sun, it must turn slightly more for the Sun to return to the local meridian.
• Solar day (mean solar day): Average time between local noons: 24 hours by definition. The actual Sun’s apparent motion varies seasonally; see Equation of Time.
• Local Sidereal Time (LST): The right ascension currently on your local meridian. It underpins the transition from RA to Alt‑Az.

Time Scales and Standards

• UTC (Coordinated Universal Time): Civil time. It is based on atomic time but adjusted with leap seconds to stay within 0.9 s of Earth rotation (UT1).
• TAI (International Atomic Time): Uniform atomic time without leap seconds. As of late 2024, TAI leads UTC by 37 seconds.
• TT (Terrestrial Time): A theoretical uniform time scale used for ephemerides; TT = TAI + 32.184 s. Dynamical equations for planetary motion are expressed in TT.
• UT1 and DUT1: UT1 tracks Earth’s actual rotation (non-uniform). DUT1 = UT1 − UTC is broadcast for precise pointing and navigation.

Practical workflow: You obtain an object’s J2000 RA/Dec, compute your LST from UTC, derive the hour angle (HA = LST − RA), and convert to altitude and azimuth for your latitude. For highest precision, fold in precession–nutation, polar motion, and refraction and parallax.

Precession, Nutation, Proper Motion, and Epochs

The sky’s coordinate grid drifts over time because Earth is not an inertial reference frame. Four effects dominate practical work:

• Precession: Earth’s rotation axis slowly traces a 26,000-year cone due to gravitational torques from the Sun and Moon acting on Earth’s equatorial bulge. The equinox moves westward along the ecliptic at roughly 50.3 arcseconds per year (about 1° in 71.6 years). This changes RA/Dec even if stars were fixed.
• Nutation: A smaller wobble superimposed on precession, primarily with an 18.6-year period linked to the regression of the Moon’s nodes. The largest nutation term is about 9 arcseconds in obliquity.
• Proper motion: Stars have their own space motions. Barnard’s Star, for instance, shifts by about 10.3 arcseconds per year, a record among bright nearby stars. Over decades, proper motion must be applied for nearby or high-proper-motion stars.
• Aberration of light: Apparent displacement caused by Earth’s orbital velocity. The annual aberration amplitude is about 20.5 arcseconds. High-precision “apparent place” calculations include aberration.

Because of these effects, catalogs specify an epoch and equinox—most commonly J2000.0—for positions. For accurate pointing “of date,” transform J2000 coordinates to the current date’s equator and equinox, and apply proper motion if significant. Large surveys and almanacs typically document the precession–nutation model used (e.g., IAU 2006 precession with IAU 2000A nutation).

J2000.0 corresponds to 2000 January 1 at 12:00 TT (not midnight). The half-day offset centers the epoch at a dynamical day midpoint.

Understanding precession clarifies familiar astronomical shifts. The “North Star” changes over millennia; today it is Polaris, but a few thousand years ago it was near Thuban (Alpha Draconis), and in ~12,000 years Vega will come close to the north celestial pole—not exactly coincident, but notably near. For practical observing in a human lifetime, precession is modest yet measurable for precision pointing, making the J2000 vs date distinction important in software and mount control.

Ecliptic and Galactic Coordinates

Ecliptic Coordinates

The ecliptic plane is Earth’s orbital plane about the Sun. The ecliptic coordinate system uses ecliptic latitude (β) and longitude (λ), measured from the vernal equinox along the ecliptic. The obliquity of the ecliptic (the tilt between ecliptic and equator) is about 23.44° at J2000 and slowly decreases by roughly 47 arcseconds per century.

Why ecliptic coordinates matter:

• Planetary ephemerides: Planet positions, solar eclipses, and occultations often live naturally in the ecliptic frame.
• Zodiacal light and meteors: The interplanetary dust cloud aligns with the ecliptic; meteor radiant maps often reference it.
• Seasonal geometry: Solstices and equinoxes are defined by the Sun’s ecliptic longitude.

Galactic Coordinates

Galactic coordinates align with the Milky Way’s disk. Galactic longitude (ℓ) starts at the direction toward the Galactic Center and increases along the disk; galactic latitude (b) measures angular distance from the Galactic plane. The modern IAU definition is tied to J2000, placing the North Galactic Pole near RA ~12h51m, Dec ~+27°, and ℓ = 0° toward the Galactic Center in Sagittarius. This frame is invaluable for mapping interstellar gas, star formation, and large-scale Galactic structure.

Transformations among Equatorial, Ecliptic, and Galactic frames are rotations on the celestial sphere. Conceptually, you rotate vectors between axes defined by the equator, ecliptic, and Galactic pole directions. Many libraries perform these transforms transparently; see Tools and Standards.

The Equation of Time and the Analemma

Mechanical clocks run uniformly; the apparent Sun does not. The Equation of Time (EoT) is the difference between apparent solar time (what a perfect sundial would read) and mean solar time (what a uniform clock keeps). The EoT arises from two effects:

• Orbital eccentricity: Earth’s orbit is slightly elliptical (eccentricity ~0.0167). By Kepler’s second law, Earth moves faster near perihelion (early January) and slower near aphelion (early July). The Sun’s apparent motion along the ecliptic therefore varies in speed.
• Obliquity of the ecliptic: The Sun’s apparent path is tilted 23.4° relative to the equator, so the Sun’s ecliptic motion projects unevenly onto right ascension (which defines mean solar time).

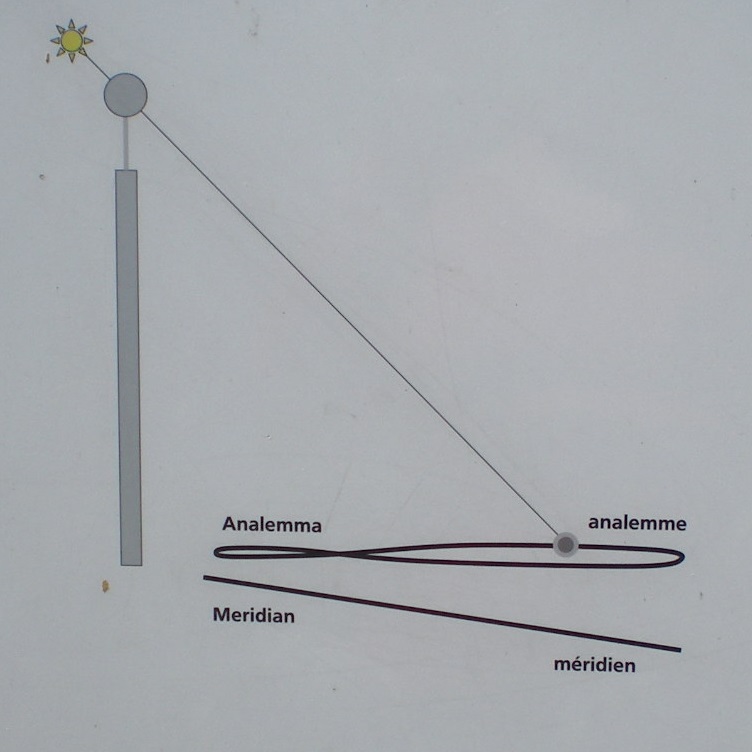
The EoT varies through the year, reaching approximately +14 to +16 minutes and −14 minutes at different dates (the precise values vary slightly year to year). When plotted as the Sun’s position at the same clock time over a year, these effects trace the famous figure‑eight analemma.

Consequences you notice on Earth:

• Solar noon drift: The moment when the Sun is highest in the sky (apparent solar noon) is not always at 12:00 local clock time.
• Earliest/latest sunrise and sunset: These do not occur exactly on the solstices; the EoT shifts them by days.

For observers planning solar work (filters required!), understanding the EoT clarifies why “noon” imaging needs the apparent, not clock, noon, and why sundials need an EoT correction plus a longitude correction from the time zone’s central meridian.

Practical Conversions: From RA/Dec to Alt‑Az

Converting catalog positions to pointing coordinates is a three-step logic. Use this roadmap—concept first, then tool support.

1) Get object coordinates of date

• Start from catalog RA/Dec, often J2000.
• Apply precession (and optionally nutation) to the target date.
• For nearby or high‑proper‑motion objects, apply proper motion (and parallax if relevant for very nearby targets).
• For solar system bodies, use ephemerides which already provide apparent RA/Dec of date.

2) Compute local sidereal time and hour angle

• From the observation time (UTC), your longitude, and Earth orientation, compute LST (Local Sidereal Time). LST = GMST + longitude (east positive). Accurate algorithms include small terms; modern libraries expose a direct call.
• Determine hour angle: HA = LST − RA (wrap to −12h … +12h for convenience).

3) Convert to Alt‑Az for your latitude

With latitude φ, declination δ, and hour angle H (in angle units), the spherical astronomy relations are:

• sin(Alt) = sin φ · sin δ + cos φ · cos δ · cos H
• sin(Az) = −(cos δ · sin H) / cos Alt
• cos(Az) = (sin δ − sin φ · sin Alt) / (cos φ · cos Alt)

Choose a consistent azimuth convention (e.g., 0° = north, increasing eastward). In code, use a two‑argument arctangent (atan2) to resolve azimuth quadrants robustly.

Refine with topocentric and atmospheric effects

• Refraction: Apply an altitude‑dependent correction, especially below ~20°.
• Topocentric parallax: For the Moon and planets, correct for your observing location on Earth rather than Earth’s center.
• Polar motion and EOP: High‑precision pointing can incorporate Earth orientation parameters to tie UT1 to LST precisely.

Many observers will never hand‑calculate these steps; however, knowing the chain helps you diagnose disagreements between star charts, apps, and mounts. If your telescope says a star is below the horizon but your app shows it above, check the time scale (UTC vs local time), location, and whether refraction is included. A quick recomputation of HA = LST − RA can immediately tell you if the object should be east (negative HA) or west (positive HA) of the meridian.

Refraction, Parallax, and Apparent Place

“Where the star appears” differs from a simple geometric transformation because of the atmosphere and your vantage point.

Atmospheric Refraction

Refraction bends light downward, raising apparent altitude. It depends on altitude, air pressure, temperature, and wavelength. Key facts:

• Near the horizon, standard refraction is roughly 34 arcminutes—about the apparent diameter of the Sun or Moon—so you can see objects that are geometrically below the horizon.
• At 45° altitude, refraction is on the order of 1 arcminute.
• Blue light refracts slightly more than red; high-precision work can account for dispersion.

Practical formulas (e.g., Bennett’s) provide useful approximations when meteorological inputs are known. For precise astrometry, models use refractivity integrals and site conditions. Planetarium software typically lets you toggle refraction on or off to match the intended use.

Topocentric Parallax

Because you observe from Earth’s surface, not its center, nearby objects shift position relative to the distant background:

• Moon: Horizontal parallax is about 1 degree (≈ 57 arcminutes), so topocentric corrections are mandatory for accurate lunar pointing and occultation timing.
• Planets: Typically tens of arcseconds depending on distance—still significant for precise pointing.
• Sun: Horizontal parallax is about 8.8 arcseconds.

Apparent vs Mean Place

Astronomical positions come in flavors:

• Mean place: Coordinates with precession applied, often excluding nutation and aberration.
• Apparent place: Includes nutation and aberration (and often light‑time corrections for planets), producing the
  “as seen” position on the sky in an inertial frame.
• Topocentric apparent place: Adds parallax and refraction for the observer’s site and conditions.

Be clear which you need. For a small telescope hop, mean place with refraction is fine. For high-precision astrometry or occultation work, use topocentric apparent place with current Earth orientation parameters.

Tools, Standards, and Reliable Data Sources

Trusted tools encode the details and keep you aligned with international standards:

• SOFA and ERFA libraries: The IAU’s Standards Of Fundamental Astronomy (SOFA) C/Fortran routines—and the open ERFA derivatives—implement time scales, Earth orientation, and coordinate transformations (precession, nutation, polar motion, etc.).
• USNO/NASA/JPL ephemerides: High‑precision solar system positions (e.g., JPL Horizons) include light‑time, relativistic corrections, and topocentric options.
• Planetarium software: High‑quality applications compute LST, RA/Dec, and Alt‑Az of date, and optionally refraction and parallax. Always verify your input location, elevation, and time zone settings.
• IAU Resolutions: For precession‑nutation and timekeeping conventions (e.g., IAU 2000/2006), consult official summaries and notes when implementing code.
• Almanacs: The Astronomical Almanac, and many national almanacs, provide daily RA/Dec, LST tables, rise/set times, and Equation of Time values.

For students and developers, a robust strategy is to validate your transformations against a reference: pick several test stars across RA/Dec and compare your Alt‑Az outputs against SOFA/ERFA or an ephemeris provider at multiple dates and sites. Differences should be at the arcsecond level (or better) if you implement the same options and models.

FAQs: Concepts and Definitions

What is the difference between RA/Dec and Alt‑Az?

RA/Dec is a global, Earth‑axis‑aligned system used to publish positions; it changes slowly with epoch because of precession and nutation. Alt‑Az is a local, horizon‑based system that depends on observer location and time. You convert RA/Dec of date to Alt‑Az using your local sidereal time and latitude; see Practical Conversions.

Why is right ascension measured in hours?

RA measures angular distance along the celestial equator, but astronomers historically linked it to time: 24 hours correspond to 360°, so 1 hour of RA equals 15°. This makes it convenient to convert a time interval to how far the sky has rotated, and vice versa.

What is Local Sidereal Time (LST)?

LST is the right ascension on your local meridian. If LST equals a star’s RA, that star is crossing your meridian (hour angle zero). LST is derived from UTC, your longitude, and Earth orientation; it advances by approximately 24 sidereal hours per sidereal day (about 4 minutes faster than solar time each day).

What does J2000.0 mean?

J2000.0 is a standard epoch used to define the equator and equinox for published positions. It corresponds to 2000-01-01 12:00 TT. Because Earth’s axis slowly moves, RA/Dec on a given date differ from their J2000 values; software can precess positions from J2000 to “of date.”

What is the Equation of Time in simple terms?

It is the difference between sundial time (apparent solar time) and clock time (mean solar time). Because Earth’s orbit is slightly elliptical and tilted relative to the equator, the Sun appears to run a bit fast or slow through the year. The offset can be more than a quarter hour either way. See Equation of Time.

How accurate is the sidereal day?

The sidereal day is approximately 23h 56m 4.0905s. Earth’s rotation is not perfectly uniform due to tidal and geophysical effects, which is why UT1 and leap seconds exist to keep UTC close to mean solar time.

FAQs: Observer and Planning Questions

How do I know when a target will be highest in the sky?

Find your target’s RA and track your Local Sidereal Time. The target culminates (highest altitude) when LST = RA. Many apps show transit times directly; otherwise, compute LST from UTC and longitude and solve for when HA = 0. Observing near transit reduces atmospheric extinction and refraction.

Why do different apps disagree on rise and set times?

They may use different assumptions: whether refraction is included, what altitude threshold defines “rise” (geometric center vs upper limb for the Sun), the exact elevation of your site, and whether the topography (hills, buildings) is considered. Time zone or DST settings can also cause offsets. Confirm inputs and check if times are for the object’s center or limb.

Do I need to worry about precession for casual observing?

Not for a single night. But if you are comparing an old printed star atlas to a modern app, small differences accumulate over decades. For accurate pointing, always use current software that computes “of date” positions; for high‑precision work, apply precession–nutation explicitly or rely on software that does.

Why is the Moon sometimes visible when it “should” be below the horizon?

Near the horizon, refraction lifts objects by roughly half a degree under standard conditions, and the Moon itself spans about 0.5°. Depending on pressure and temperature, you can sometimes see it when it is geometrically just below the horizon.

What are ecliptic and galactic coordinates good for in practice?

Ecliptic coordinates are natural for planetary observing and understanding where the zodiacal light will be brightest. Galactic coordinates are ideal when you plan a Milky Way survey or map star clouds and nebulae along the disk. Your app can switch among frames; see Ecliptic and Galactic Coordinates.

Why does my equatorial mount track with just one motor?

By aligning one axis with Earth’s rotation axis, the mount cancels Earth’s spin with a constant sidereal-rate motion on that axis. This holds RA fixed. Any residual drift is due to polar misalignment, refraction, flexure, or unmodeled motions; periodic error correction and good polar alignment mitigate these effects.

Conclusion

Celestial coordinates and astronomical time are a single tapestry. The choice of frame—horizon, equator, ecliptic, or galaxy—aligns your math with the physics of what you study: Earth’s spin, Earth’s orbit, or the Milky Way’s disk. Time scales—sidereal, solar, and atomic—anchor those frames to observations and ephemerides. Once you internalize the relationships among RA/Dec, Alt‑Az, LST, and the corrections in refraction and parallax, the sky becomes predictable and navigable.

Keep a few practical anchors: use J2000 for catalog work but precess to date for pointing; compute LST and hour angle to understand where a target is relative to your meridian; observe near transit for the steadiest views; and lean on robust standards and software (SOFA/ERFA and ephemerides) when precision matters. If this overview sharpened your celestial navigation, explore related deep dives on coordinate transformations, Earth orientation, and ephemerides—or subscribe for future articles that build on these foundations.